 Dr.-Ing. Gottlieb Strassacker
Dr.-Ing. Gottlieb Strassacker
Dozent an der Universität Karlsruhe in Ruhestand |
Vertiefung und Ergänzung der komplexen Rechnung
In "Ohmgesetz komplex und einfache Filter" habe ich die Berechnung komplexer Widerstände, komplexer Leitwerte und der Spannungs-Übertragungs-Verhältnisse einfacher Filter vorgestellt. Komplexe Rechnung ist aber umfassender. Mit ihr kann man auch die Phasenbeziehungen verschiedener Sinusschwingungen und die Frequenzen von Leistungen systematisch berechnen. Aber komplexe Rechnung gilt nur bei linearen Systemen. Das sind Systeme mit linearem Zusammenhang der von einander abhängigen Größen mit linearen Kennlinien. Mathematisch ausgedrückt: Die beschreibenden Differentialgleichungen sind linear. Wir wollen jetzt die komplexen Größen eingehender betrachten. Der Deutlichkeit wegen unterstreichen wir wieder komplexe Größen, um sie von reellen zu unterscheiden. Die Wechselströme und -Spannungen schreiben wir mit kleinen Buchstaben.Eine komplexe Amplitude, z.B. die einer Spannung û, ist das Produkt aus reeller Amplitude û mit ejα, den Satz des Moivre wenden wir gleich mit an:
(1) û = û ejα = û [cos(α)+j sin(α)]
Entsprechend gilt für komplexe Momentanwerte mit Argument α = ωt:
(1a) u(t) = ûejωt = û [cos(ωt)+j sin(ωt)]
Sind zwei Spannungen gegen einander phasenverschoben, d.h. ihre Sinuskurven sind nicht deckungsgleich, dann wird das eine Argument noch durch einen so genannten Nullphasenwinkel, z.B. φ ergänzt. Ist ein Nullphasenwinkel vorhanden, dann beginnt die Schwingung im Falle des Sinus bei t = 0 nicht mit null, sondern mit sinφ, im Falle des Cosinus nicht mit cos0o=1, sondern mit cosφ < |1|.
Beispiel des komplexen Momentanwertes einer Spannung mit Nullphasenwinkel:
(2) u(t) = ûej(ωt+φ) = û [cos(ωt+φ)+j sin(ωt+φ)]
Von den jeweils beiden vorhandenen harmonischen Schwingungen Sinus und Cosinus wird im Ergebnis nur eine benötigt, beide sind jedoch innerhalb des komplexen Rechenganges erforderlich, um das Ergebnis richtig ermitteln zu können, was durch folgendes Beispiel deutlich wird. Zuerst aber ist noch die Umwandlung von kartesischen in Polarkoordinaten zu zeigen:
Wir gehen von einem komplexen Widerstand aus: Z = R+ jX . Er soll umgeformt werden in Polarkordinaten, d.h. in Betrag mal ej Winkel:
(3) R+jX = (R2 + X 2)1/2 ejarctan(Imaginärteil/Realteil)
Steht eine komplexe Größe im Nenner, so gilt entsprechend:
(4) 1 / (a + jb) = (a2 + b2) -1/2 · e-jarctan(b/a)
Es soll noch gezeigt werden, wie die komplexen Widerstände jωL und 1/(jωC) aus den komplexen Augenblickswerten von Strom und Spannung zu Stande kommen. Unterstrichen sind wieder die komplexen Größen. Zuerst der komplexe Widerstand einer idealen d.h. verlustlosen Spule der Induktivität L:
(5) uL(t) = L diL(t) / dt mit iL(t) = îLejωt ergibt: uL(t) = jωL · iL(t)
Man sieht, der Quotient zwischen den komplexen Augenblickswerten von induktiver Spannung und Strom ist der komplexe Widerstand jωL. Dieser komplexe Widerstand ist auch der Quotient zwischen den komplexen Amplituden von Spannung und Strom. Jetzt kommen wir zum kapazitiven Widerstand 1/jωC eines idealen, d.h. verlustlosen Kondensators:
(6) iC(t) = C duC(t) / dt mit uC(t) = ûCejωt ergibt: iC = jωC · uC(t)
Hier schreiben wir der Deutlichkeit halber die Quotienten aus Spannung und Strom sowohl für Momentanwerte als auch für komplexe Amplituden auf:
(7) uC(t) / iC(t) = ûC ejωt / îC ejωt = 1 / jωC
Man sieht, im mittleren Term von Gl.(7) steht im Zähler und Nenner ejωt, was sich wegkürzt, woraus erkennbar ist, dass der Quotient der Momentanwerte gleich dem Quotienten der komplexen Amplituden gleicht.
Beispiel 1 aus der Elektrotechnik, ein KLingeltrafo
Nahezu jede Wohnung enthält einen Klingeltrafo. Das ist ein Transformator, der die Wechselspannung von 230 V in eine niedere Spannung von 6 oder 8 V herunter transformiert. Mit der niederen Spannung kann man einen Klingel-Stromkreis betreiben. Ein solcher Klingeltrafo hat einen Eisenkern, dessen Schenkel die Primärwicklung mit hoher Windungszahl und die Sekundärwicklung mit geringer Windungszahl aufnimmt. Denn die Spannungen an den Wicklungen des Trafos verhalten sich in guter Näherung wie die Windungszahlen: 230 V / 8 V = Primärwindungszahl / Sekundärwindungszahl = w1 / w2.
Die längste Zeit des Tages ist die Klingel ohne Inanspruchnahme, d.h. der Trafo arbeitet im Leerlauf mit i2=0; denn so lange kein Klingelknopf betätigt wird, fließt auch kein Strom im Sekundär- also im Klingelstromkreis i2. Wir betrachten diesen Zustand des Leerlaufes. Dafür gilt näherungsweise als elektrisches Ersatzbild, das den Betrieb des leerlaufenden Trafos beschreibt, bestehend aus einer Spule mit der Induktivität L und dem Wicklungswiderstand R1. In dem Augenblick des Klingeldrückens haben wir auch i2 ungleich null. Das nachfolgende Bild zeigt links den prinzipiellen Aufbau eines Klingeltrafos und rechts daneben das einfachste der vielen möglichen elektrischen Ersatzbilder:
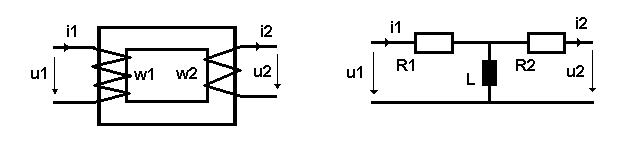
Im Leerlauf wirken also nur der Tiefpass aus R1 und der primären Wicklungsinduktivität, die hier mit L bezeichnet ist. R1 ist nichts anderes als der ohmsche Widerstand der Primärwicklung. Der im Leerlauf vorhandene Strom i1 und damit auch die Verlustleistung an R1 sind so klein, dass der Energiezähler (Stromzähler) nicht anspricht. Daher verlangen die Stromversorgungsunternehmen eine Grundgebühr, in der auch diese Verlustleistung inbegriffen ist.
Da der Klingeltrafo zu mindestens 95 % des Tages im Leerlauf arbeitet, genügt es uns, diesen Betriebszustand mit R1 und L zu betrachten. Dabei wollen wir die Phasenverschiebung zwischen Eingangsspannung u1(t) und i1(t) formelmäßig berechnen. Wir verwenden dazu komplexe Amplituden:
(8) û1 = î1 · Z ausführlicher: û1 = î1 · (R1+ jωL)
Eine Phasenverschiebung entsteht durch (R1 + jωL). Wir formen diesen Term um in Polarkoordinaten, also in Betrag und Winkel:
(9) (R1 + jωL) = (R12 + ω2 L2)1/2· ej arctan(ωL/R1)
Abschätzung der Werte
Bei einem Klingeltrafo ist in der Regel der ohmsche Wicklungswiderstand der Eingangsseite R1 sehr klein. Er möge in etwa bei 3 Ohm liegen. Dagegen ist der induktive Wicklungswiderstand der Eingangsseite groß. Je nach Bauart und Alter liegt der Leerlaufstrom (der Primärseite) bei 15 bis 30 mA. Nehmen wir einen Mittelwert an von grob 20 mA. Dann kann der Eingangswiderstand bei etwa 230 V / 20 mA liegen, das sind etwa 11,5 kΩ. Da mit der Frequenz des Stadtnetzes von 50 Hz gearbeitet wird, ist L = |Z| / ω = 11,5 kΩ / (2π50/s) = 36,6 mHenry. Nun zur Phasenverschiebung:
(10) arctan(ωL / R1) = arctan(11,5 kΩ / 3 Ω) = arctan 3833; φ = 89,98o,
Die gesamte Phasendrehung zwischen Eingangsspannung und Eingangsstrom ist somit fast 90o. Das kann man in Verbindung mit Spannung und Strom auch so anschreiben:
(11) û1 = î1 · (R12 + ω2 L2)1/2 ej 89,98o
Wir sehen, dass die komplexe Amplitude der Eingangsspannung û1 und damit auch u1(t) dem Eingangsstrom î1 und damit auch dem Momentanwert i1(t) um fast 90o voraus eilen. Das ist immer dann der Fall, wenn eine Wechselspannung an eine fast oder ganz verlustlose Spule angeschlossen ist.
Leistungsberechnung am Klingeltrafo
Verlustleistung, die bezahlt werden muss, ist grundsätzlich definiert als zeitlicher Mittelwert der Leistungsschwingung P(t). Da aber unsere primäre Trafospule des oben besprochenen Klingeltrafos fast verlustfrei ist, ist auch der zeitliche Mittelwert von P(t) in etwa gleich null. In anderen Fällen ist die Schwingung P(t) über die Zeitachse mehr oder weniger nach oben verschoben, so dass ihr zeitlicher Mittelwert größer null wird.
Praktisch berechnet sich die Verlustleistung bei harmonischen Schwingungen aus dem Produkt der Effektivwerte von Spannung und Strom multipliziert mit cosφ. Will man aber die Momentanwerte der Leistung P(t) berechnen, so sind auch die Frequenzen mit einzubeziehen. Wir berechnen P(t) komplex mit den allgemeinen Formelzeichen:
(12) P(t) = (û1 / 21/2) ej(ωt+φ)· (î1 / 21/2) ejωt = û1î1 ej(2ωt+φ) / 2
Wir sehen, die Frequenz der Leistungsschwingung P(t) ist doppelt so groß wie die Freqenz von Spannung und Strom.
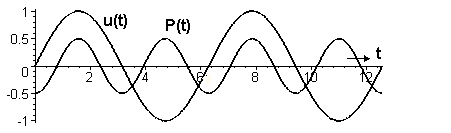
Die Leistungs- schwingung P(t) hat doppelt so große Frequenz wie die Spannung u(t). Die Amplituden von u(t) und P(t) wurden willkürlich gewählt. Man kann diese beiden Amplituden hier auch nicht vergleichen mit einander, denn Spannung wird gemessen in Volt, Leistung wird gemessen in Watt.
Der Deutlichkeit wegen ist P(t) im Bild gegenüber der Spannung u(t) um π/2 nacheilend. Das ist real dann der Fall, wenn der Strom um π/2 gegen die Spannung nacheilend ist, z.B. an einer verlustlosen oder sehr verlustarmen Spule, wie dies bei dem Klingeltrafo der Fall war.
In den Momenten, in denen der Klingelknopf gedrückt wird, überträgt der Trafo auch Strom auf seine Sekundärseite, um die Klingel zu betreiben. Die Phasenverschiebung zwischen Eingangsspannung und Eingangsstrom ist dann nicht mehr 89,98 Grad, sondern geringer, abhängig vom Stromverbrauch der Klingel.
Beispiel 2, ein Tiefpass
Tiefpässe sind dazu geeignet, Spannungen ab einer gewissen Frequenz, die man als Grenzfrequenz bezeichnet, mehr und mehr zu bedämpfen. Um den Rechengang deutlich zu machen, legen wir eine reelle Sinusspannung u1(t) = û1 sin(ωt) an einen Tiefpass bestehend aus R im Längszweig und C im Querzweig, nach folgendem Bild:
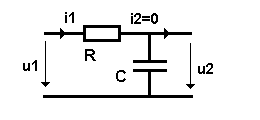
Wir wollen sehen, welche Spannung nach Betrag und Phasenwinkel am Ausgang des Tiefpasses zu erwarten ist. Dazu müssen wir die gerade gegebene reelle Eingangsspannung für den Rechengang komplex anschreiben: û1 = û1ej(ωt).
Diese komplexe Eingangsspannung wird eingesetzt in die komplexe Spannungsübersetzung des Tiefpasses. Letztere ist ja ohne die Zeitabhängigkeit:
(13) û2 / û1 = (1 / jωC) / ( R + 1 / jωC ) = 1 / (1 + jωRC)
Nun sind wir auch schon fast fertig. Allerdings ist die rechte Seite der Gleichung noch nach Betrag und Winkel richtig anzuschreiben, wie dies bei Polarkoordinaten üblich ist. Man beachte, das Minuszeichen in den Exponenten zeigt, dass es sich um Größen im Nenner handelt:
(14) 1 / (1 + jωRC) = [12 + (ωRC)2] -1/2 · e-j arctan(ωRC) mit φ = - arctan(ωRC)
Wir bringen û1 von Gl.(13) auf die rechte Seite und setzen dafür unsere komplex angeschriebenen Momentanwerte der Eingangsspannung, siehe Gl.(1a), ein; dann ist auch die Sekundärspannung links des Gleichheitszeichens ein Momentanwert. Mit anderen Worten: Durch Multiplizieren der komplexen Amplituden mit dem Zeitfaktor ejωt gehen die komplexen Amplituden in komplexe Momentanwerte über:
(15) u2(t) = û1ej(ωt) · [12 + (ωRC)2] -1/2 · e-j arctan(ωRC)
Jetzt sind die Winkel von ejωt und e-j arctan(ωRC) zusammen zu bringen, wobei -arctan(ωRC) = φ ist. Dazu sollten wir wissen, dass ejωt· e - jφ = ej(ωt-φ) ist:
(16) u2(t) = û1· [1 + (ωRC)2] -1/2· ej(ωt-φ); φ = -arctan(ωRC)
Damit ist die komplex hergeleitete Lösung der Aufgabe fertig. Wir hatten aber zu Beginn unseres Beispiels eine reelle sinusförmige Eingangsspannung u1(t) angenommen. Daher dürfen wir jetzt aus der komplexen Endlösung auch den Sinusteil als reelles Ergebnis entnehmen; die komplexe Lösung nach Gl.(16) enthält ja nach dem Moivreschen Satz, ejβ = cosβ + j sinβ, beide Anteile. Das reelle Endergebnis ist somit:
(17) u2(t) = û2· sin(ωt-φ) = û1· [1 + (ωRC)2] -1/2· sin(ωt-φ) mit φ = arctan(ωRC)
Diskussion des Ergebnisses
Wir sehen, dass die Amplitude û2 durch die Nennerwurzel bei
û1, also durch [1 + (ωRC)2]-1/2 verringert wird. Dabei kann ωRC
Werte zwischen 0 und unendlich annehmen. Zugleich kann sich der Winkel φ für
0 < ωRC < unendlich zwischen 0 < φ < 90o bewegen.
Grenzwerte:
Mit ωRC = 0 ist auch φ = 0;
ωRC = unendlich: φ = 90 Grad und û2 = 0 wegen des Nennerausdrucks [1 + (ωRC)2]1/2.
φ ungefähr null Grad bedeutet, dass die Schwingungsverläufe von u2(t) und u1(t) gleichphasig, also deckungsgleich sind. Bei φ = 90 Grad eilt u2(t) gegen u1(t) um 90 Grad nach.
Praktisch bedeutet ωRC = 0 und damit auch φ=0 Gleichspannung, wobei sich der Kondensator einmalig aufgeladen hat, wonach kein Strom mehr fließt. Dieser einmalige Vorgang ist Anlass, auf so genannte Ausgleichs- Übergangs- oder Einschwingvorgänge aufmerksam zu machen. Sie treten jeweils während Bruchteilen von Sekunden beim Einschalten einer Spannung auf, um den Übergang zum stationären oder Dauerzustand einzuleiten. Ihr Verlauf ist abhängig vom Moment des Einschaltens. Danach erst fungiert das mit komplexer Rechnung ermittelte Rechenergebnis. Diese nur kurz andauernden Ausgleichsvorgänge werden durch Lösen der beschreibenden Differentialgleichungen berechnet. Die Theorie dazu ist jedoch so umfangreich, dass sie hier nicht besprochen werden kann.
zurück zur Übersicht